Fractions are a Royal Pain in Imperial
Updated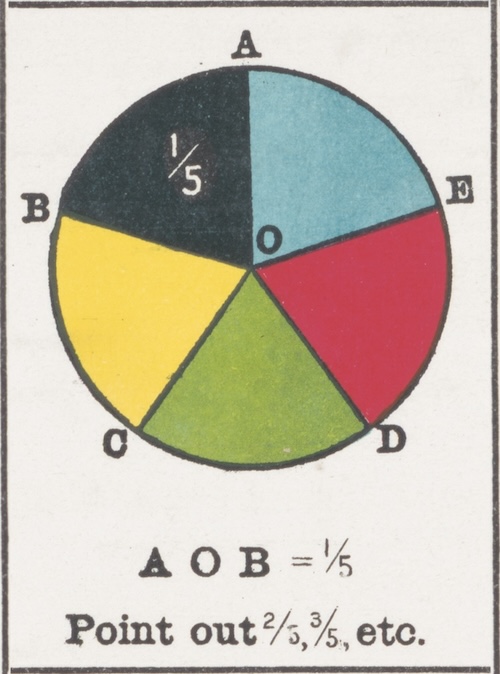
What is a fifth of an imperial yard? Answering that question requires a bit of math.
Most likely the person asking the question expects the answer in familiar fractional inches where the fraction is some multiple of 1/2, 1/4, 1/8, 1/16, or 1/32. Below are the simplest possible steps to convert 1/5 yard into proper fractional inches.
| Value | Step |
|---|---|
| 1/5 yard | What's 1/5 of a yard? |
| 36/5 inch | Multiply by 36 to convert to inches. |
| 7 inches + 1/5 inch | Extract whole inches for simplicity. |
| 7 inches + 1/5 inch × 32/32 | Assume at most 1/32 precision. |
| 7 inches + (32×1/5)/32 inch | Solve for the numerator. |
| 7 inches + 6.4/32 inch | Do math to calculate numerator. |
| 7 inches + 6/32 inch | Round to nearest 1/32 of an inch. |
| 7 inches + 3/16 inch | Reduce fraction for convenience. |
| 7 3/16 inches | Presto! We have the proper fractional inch answer. |
Below are the answers for other common imperial lengths. Can you do the math required to get the correct answer?
| Imperial Question | Answer |
|---|---|
| What's 1/5 of an inch? | 3/16 inches |
| What's 1/5 of a foot? | 2 13/32 inches |
| What's 1/5 of a yard? | 7 3/16 inches |
| What's 1/5 of a mile? | 1,056 feet |
Metric is easier by a country kay. For example, there are 10 mm in a cm, so 1/5 of a cm is 2 mm.
| Metric Question | Answer |
|---|---|
| What's 1/5 of a cm? | 2 mm |
| What's 1/5 of a meter? | 20 cm |
| What's 1/5 of a km? | 200 m |
0.3333333333
Some imperial zealots obsess about 1/3 because they incorrectly believe that dividing by 3 is incompatible with metric. When they pull the 1/3 stunt, simply ask them what's 1/3 of a cup?
| What's 1/3 of... | Answer | |
|---|---|---|
| a cup in ounces? | 2.666 ounces | Awkward |
| a cup in tablespoons? | 5.333 tablespoons | Awkward |
| a U.S. dollar? | 33¢ |
While the imperial zealot is stewing over the awkwardness of 1/3 of cup, ask if they would have trouble figuring out 1/3 of a U.S. dollar? The U.S. dollar is metric and there's never been a world financial meltdown because someone couldn't do division on a dollar.
Answering the 1/3 question in metric is not a problem. Depending on the desired precision, the answer to what's 1/3 of a meter is either 33 cm or 333 mm. Easy peasy.
Even if you need to pull out a calculator, metric is still far less effort. Let's say your measurement is 1,107 mm. You punch 1,107 into your calculator and divide by 3, and you're done in one operation.
| What's 1/3 of... | Calculation | |
|---|---|---|
| 1,107 mm? | 1107 ÷ 3 = 369 | |
| 43 5/8 inches? | ((5 ÷ 8) + 43) ÷ 3 14.54 14 ?/8 | Awkward |

The imperial equivalent is 43 5/8 inches, so you punch 5 into your calculator and divide by 8 then add 43 then hit equals and finally divide by 3. You get 14.54 inches, but sadly your tape measure does not have tick marks for 54/100 of an inch. Doh! What a royal pain for something so trivial.
The Proof Is in the Pudding
Fractions are such a pain in imperial that entire professions switched to incompatible "decimal" types of imperial units just to avoid imperial fractions. Land surveyors use decimal feet. Machinists use decimal inches. Meanwhile, carpenters use "customary" fractional inches.
| Profession | Imperial Units | Compatible |
|---|---|---|
| Surveyor | Decimal Feet | |
| Machinist | Decimal Inches | |
| Carpenter | Fractional Inches |
The consequence of using imperial units is that surveyors, machinists, and carpenters cannot share each other's measurements. Surveyors and machinists do math every day, and they choose to avoid imperial fractions not because they are too dumb to do fractions but because they are smart and need to be efficient.
Time is money, and imperial is on the wrong side of the equation.
Denominators are Sneaky
How many inches is:
(7 3/4" + 5 7/8") × 2
Doing basic math operations with fractional inches, is cumbersome, but denominators can be quite sneaky even if you're not doing math operations.
How many times have you made a measurement like 9 5/16" and then gone to make
the cut only to have to return to measure again because you forgot if it was
9 5/8" or 9 5/16"?
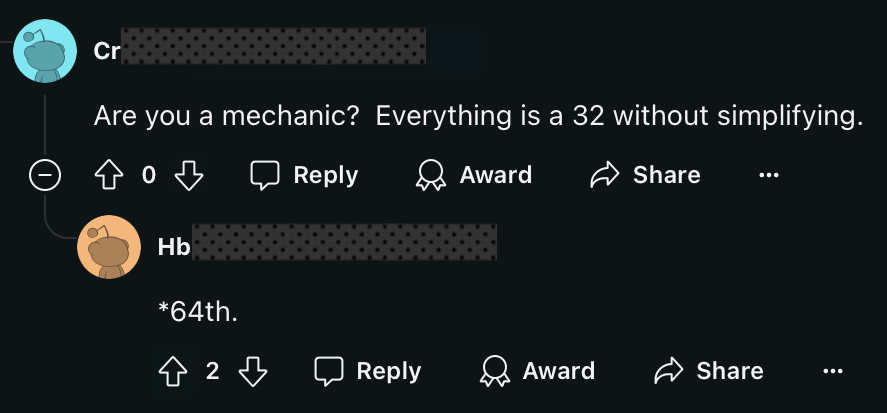
Because of the small extra cognitive load dedicated to remembering the denominators, you can hold fewer imperial measurements in your head simultaneously than metric measurements. Going metric means you have to write down measurements less often saving you a few seconds here and there so you're a bit more productive.
 Google Maps
Google Maps